II.
Serial Structures as Fragmentation of the Familiar
In
this part of the Essay, I begin with a technical discussion of some aspects of
the construction of the piece, Sand. I then move on to a discussion of
important motivations for constructing some of my pieces in this way.
II.i.
19 Tone Equal Temperament
I start at the
level of tuning. This piece is in
19-tone equal temperament.[1] For me, the primary reason for this is
exploratory: interesting
microtonal systems and tunings are an aspect of music that, without the
computer, have been off-limits for most composers until recently. Those who have ventured into this
domain prior to the last decade or so, have been intrepid figures indeed, and have had to devote much of their
time and energy to such activities as building instruments, developing and testing theories of
intonation, and so on. But this
has changed quite a bit in the recent past. The computer has made it possible to explore and compose for
virtually any tuning or microtonal system that could be conceived: from Just Intonation, to spectral
techniques, to the exploration of alternative equal-temperaments, to un-equal
temperaments (such as the predecessors to 12-tet including various forms of
meantone, Werckmeister, tunings used in various world-musics, etc.), or even sets of randomly generated
scales.[2]
I decided that
since I was working on a piece of
computer music, free of the
intonational limitations of commonly available acoustic instruments, I might as well take advantage of the
medium and write in a tuning not available on those instruments.
It
turns out that 19tet worked out well for me, since I was planning a work emphasizing the the [0 1 3]12 trichord.[3] This has always been a favorite sound
of mine, the minor third is one of its intervals, and 19tet has nearly perfectly Just-Tuned minor 3rds.[4]
My relationship to 19tet, at the point when I decided to use it, was
virtually nil.[5] In an attempt to be sort of honest
about this, I took sounds that I liked from 12tet, and thought about warping
them in various ways into 19tet.
Thus, for example, [0 1 3]12 can be
interpreted, so to speak, in 4 different ways in 19tet:[6]
("≈"
means (here) "sounds approximately like.")
[0 1 3]12 ≈ [0 2 5]19
or [0 1 5]19 or [0 1 4]19
or [0 1 3]19
Some
possible instantiations in pitch notation :
[C Db Eb]12 ≈ [C Db Eb]19 or [C C# Eb]19 or [C C# D#]19
or [C C# D]19
The above are listed in order of decreasing
similarity; [0 1 3]19 I
find too harsh to use as a quasi-[0 1 3]12, most of the time.
A
chord which is perhaps the main harmonic unit of this piece, and which cotains
this set, also undergoes this
"interpretive" process:
[0 2 4 7 8 10]12
≈ [0 3 6 11 13 16]19 or
[0 3 6 11 12 16]19
or [0 3 6 11 12 15]19
In
pitch notation, possibly:
[C D E G Ab Bb]12 ≈ [C D E G Ab Bb]19 or [C D E G G# Bb]19
or [C D E G G# A#]19
II.ii.
Serial Structure
I built a
19-pitch-class row saturated with the [0 1 3]12 translations:
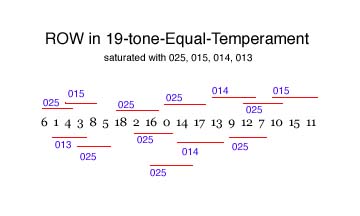
Out of that I built an array or compositional design.[7]
The
following is the basic building-block of the array; 6 lines by 6 agreggates. If the row given in Example 1 is
considered the "prime" form, then this building-block contains two
instances of P, two instances of I, and one instance each of R and RI:

To
form a larger structure I did the following: instantiate 19 different transpositions of this basic block
(in other words, all the possible transposition levels of it).[8] By concatenating these 19 blocks
horizontally, according to a certain set of rules[9],
and swapping pitches between blocks,[10]
I can obtain an array that contains at least one instance of each of the 19
transpositions of each of the 4 canonic row-forms (P, I, RI, R); and where the partitioning
scheme for each 19-tone aggregate is unique.[11] That produces a 114-agreggate
structure.
For
the pitch-structure of the piece, however, I use approximately half of that
structure. See near the
bottom of
this page
for this
60-aggregate array structure.
Now
imagine that structure in canon with itself:

The
pitch structure of the piece Sand
consists of this, but with
the "dux" structure
realized on the music's surface as unspatialized notes (i.e. un-reverberated,
or "in your face"), and
the "comes" structure as "spatialized" notes
(reverberated.) Registrally,
they are intertwined, as shown in this example:

Again, see the bottom of
this page
for this complete contrapuntal pitch structure.
The intertwining of unspatialized (the dux array) and spatialized (the comes array)
lines in each register allows for a wide variety of melodic, textural
and harmonic interpretations on the musical surface. What's most interesting for me as a composer about these
intertwined lines, is to forget about what those lines mean and where they came
from individually: I spin music
out of the composite, and then listen to how the fact that some of the notes
are spatialized and some aren't "skews" the music for my ear, perhaps
in some bizarre way. Using the
interface described in Part I, the user has the choice of perspective: they may listen to the composite line,
or break it apart into its two constituent components[12],
thus enabling the perception of new and different lines, or hearing the
composite line in a heretofore unnoted, dissected way.
II.iii.
Drones and Virtual Drones
In
Sand, a drone is usually present
underneath (or in the midst of) the contrapuntal web of music, with which the
pitches in the counterpoint
associate and form what I feel are real, perceptible, pitch
relationships. This was inspired
largely by Indian raga music, where certain notes' relationship to the drone becomes a matter of almost
ecstatic importance. An example of
drones in a serial context is Stockhausen's Licht cycle of
"operas." In those
works, a drone might be a note, a dyad,
a complex chord, or even a texture.[13]
Although
throughout Sand a drone is almost
always present as a way for the listener to form pitch-relations in their
ear/minds, (whether or not I was thinking consciously of these relations as I
composed), in certain sections of
the work, I composed the music
quite intentionally so that the counterpoint would seem to be intensively "feeling
its way around" the drone.
Section 3 of the work is one example of this.
I
enriched the pitch structure even further by the use of what I call
"virtual drone notes" that infiltrate the fundamental contrapuntal
structures detailed in the preceding sections of this chapter.
I
began using virtual drones in two chamber music works I wrote, where I was experimenting with working
aspects of spectral music into my own musical language. Simply put, the pitches of a certain
fixed spectral chord(s) tend to "hang around," and "be available
for use anytime" during a given section of a piece, while a serial
counterpoint is being unfolded.
Here is an example from my piano trio Quiet Play
of Lights. The basic (12tet) contrapuntal array for this fragment is
shown here:
|
violin--short notes |
|
A D |
|
violin--long notes |
|
F# C# E
G Eb C F
Bb Ab |
|
piano
--short notes |
E G# E G# B |
|
|
piano--long notes |
|
|
|
'cello--short notes |
Eb
C D# C# F# |
|
|
'cello--long notes |
|
B |
The spectral chord[14]
whose members are available for use is as follows:

Here is what
happens in the referred passage of the Trio:

"Virtual
drone" seems an appropriate title, since the spectrum (the chord of
pitches) is not actually droning, but making its presence felt constantly
nonetheless.
In
Sand, the virtual drones are not
usually complex spectra[15]
as in the Trio, but simply overtones of the current
actual-drone pitch. I usually
stick to the first few partials--those are the notes available at any time to
"infiltrate the counterpoint."
When I intertwine
all of these possibilities: spatialized pitches, unspatialized pitches, virtual drones and adjacent registers,
I can create a quite flowing melodic product. Some examples in Sand include the second half of Section 13, the middle of
Section 23, the opening of Section 35, or the "squished" homage to
Schoenberg at Section 62.
II.iv.
Aurally Sensitive Pitch-Class Set Composition
Let
us return to that chord I mentioned earlier, and talk a bit about harmony:
[0 2 4 7 8 10]12 ≈ [0 3 6 11 13
16]19 or [0 3 6 11 12
16]19
or [0 3 6 11 12 15]19
This set, and its subsets thereof, are the
"default" array parser units in Sand.
Here
is one agreggate-partition of the array:

Here
it is, along with some "virtual drone" pitches, parsed by [0 3 6 11 12 16]19:
EXAMPLE [16]

A
problem I have had with set-theoretic ways of thinking and working in the way
they have been, for the most part, taught to me, is that all sets are treated
as equal in terms of their aural recognizability them by ear. This is not corroborated by my own
perceptions. For example, many of
us can recognize an octatonic sound, a diatonic sound, or a hexatonic sound in
a piece or passage almost instantaneously;[17]
on the other hand, To hear the [0 1 2 5 7 t]12-ish-ness of a passage
instantaneously and intuitively is quite another matter. Other considerations are often
left out of discussion as well, such as:
what's in the bass, how
chords are spaced, the sound of a
set as used melodically as opposed to harmonically, etc.
In
my piece, I set some rules for myself, vis a vis using this 6-note sonority. First, set-theoretically-speaking, it only occurs in "prime
form", never inversion.
Second, I try to have it appear in "root position" as much as
possible. I see it, in short, as
an entity that is an approximation of a set of overtones, and it will be most
audible as such when it appears un-"inverted," in all (including the traditional
vertically rotational) senses of the word.
The [0 3 6 11 12
15]19, or [C D E G G# A#]19 version of this chord, is the closest in sound (in 19tet) to
a Justly-Tuned chord of overtones
8:9:10:12:13:14. This chord
appears most obviously, explicitly Justly Tuned, in the first "drone
section" of the piece (Section 4), (the "drone sections" are occasional sections of the piece
devoted entirely to "solos" of the drone layer).
The
following is a sketch of Section 5-6 of the work, showing [0 3 6 11 12 15]19 parsings:
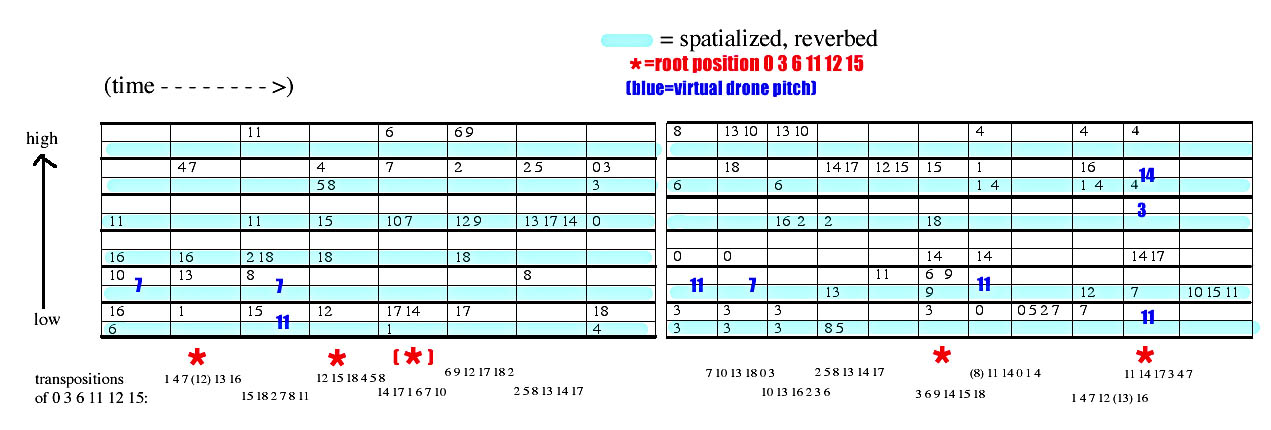
Listening
to these sections, the
"root-position" versions of the chord come out quite clearly.
II.v.
Fragmentation of the Familiar
In one strand of
my composing, which I engaged in this piece, I enjoy using serial methods---even total serial
methods. It's not a desire
for unity or coherence that impels me to work in this way. In fact, it's often quite the
opposite--the desire to put myself in a situation where I can contradict any
unifying force that may be inherent in these structures. I am attracted to
possibilities of contradictions.
Steve
Reich often[18] tells this
story: Berio was teaching him
composition, and he (Reich) brought in his obligatory 12-tone piece, which was,
none the less, quasi-tonal, composed out with triads, etc., and Berio said to
him "If you want to write a
tonal piece, then why don't you
just write a tonal piece?" To
Berio, (and, I suppose, to
Reich), I pose the question,
"But why not write a serial
piece that is 'trying to be tonal'?"
Let
us open this into a broader field;
we replace the word tonal by the concept of the familiar:
aspects, elements, or hallmarks, surface or structural, of a familiar
musical language(s). We replace
the concept of "trying to be tonal" by the concept of a music where fragments of the familiar
are torn out of context and
juxtaposed, glued, weaved, and sewn together often in interesting, emotionally
and viscerally jarring ways, that might shed new light on the character of
these fragments.
On an internet discussion group I take
part in, George Secour wrote:
"Trouble is, even if one chooses to ignore the principles of
musical acoustics and mathematical relationships, they are still there. So the pantonal [or atonal] composer is something like an
architect designing a building,
but ignoring the laws of physics."[19]
I would like to
quibble with the word "trouble".
Let us temporarily posit two points of view about composition, aspects
of which I've seen rearing their heads now and then in the various musical
communities I run around in. The
two could be crudely represented with some stereotypical quotations. For mnemonic clarity, let us identify
the two speakers as PAT and NIKY[20]:
PAT: "Art
is based on [laws of] nature." "Art should emulate nature."
"art should be made following your intuition." "The theory of ______ models
intuitive instincts of a musically sensitive individual, therefore you're wasting your time if
you don't follow its dictates."
NIKY: "All
art is arbitrary." "All
art is basically artificial." "Many sounds we find sonically and
musically interesting are artificial, inharmonic, stochastic, etc." "The
mind can learn any algorithm if you pound it in long enough." "Art is
mostly based on artificial cultural inheritances, environmentally
begotten, which are not
necessarily ingrained in anyone's mind permanently. The mind is in many (most) ways a blank slate. If all musical systems are basically
artificial, why not invent or expand on more of the same, and get on with composing?"
Rather than being hopelessly oppositional, I like to think of these two schools of thought as
intimately bound together in a fascinating way.
The first possibility is that NIKY will conceptualize or structure
his/her compositions in ways which seem to have little relation to what the ear
(even the composer's ear) can realistically perceive. But NIKY's arbitrary compositional systems leave room for
the operation of intuition, so
that when these materials are deployed on the surface of a composition, to make
a piece of music happen, those
natural instincts touted by PAT come in to play, desperately attempting to deploy NIKY's
recalcitrant, cognitively/acoustically disobedient materials in some way that,
if only provisionally, locally, in different ways at different instants,
satisfies the desires of those instincts.
The result is a music where--again--fragments of the familiar---broken-off
chunks of familiar progressions, forgotten harmonic entities, tonal chords,
simple voice-leading progressions and so on---are juxtaposed in twisted, novel
fashion, warping and changing our perspective on those familiar objects in unexpected
ways.
Another possibility is the case of "hard-core algorithmic"
music, where some kind of process or generating system is set up, seeded, and
the piece, as it were, writes itself. . . . . in this case, it is in our ears, the ears of the listener, where
this recognition of the familiar takes place.
In either case, the way we parse through such pieces, looking for some
vague cognitive signposts--gradually expanding registers, step-wise bass lines,
serendipitous fragments of tonality bridged by walls of impenetrable
chaos--this ad hoc parsing is fascinating for me--to experience as a listener,
and to try to facilitate in my music, as a composer.
In a way, these kinds of pieces are written in a higher-level language,
in the computer-science sense of the term, because these little bursts of the familiar, these
fragile handholds that we grab
onto to "survive" as listeners, are often like signifiers, standing
for whole passages of music in more traditional musical environments.
Late in Babbitt's 2nd Piano Concerto, (mm. 507-510) a swirling chaos of notes seems somehow
to magically coalesce into C# Major,
so strongly that the passage seems to me to be the "climax" (a very little hill in this very flat
piece) of the work.
At another point in this piano concerto, (mm. 203-204) there is a series of what sound
like chromatically descending
clusters, with the pitches distributed around the ensemble, in the midst of
other activity--this chromatic descent, as something vaguely familiar or simple
to me, is what I "grab onto" in this part of the piece.[21] I enjoy the feeling, while listening,
of not knowing quite what to do or what to grab onto, mentally and emotionally,
in what I'm hearing.
These experiences were probably not intended by the composer (though
Babbitt's music in particular is filled with triadic arpeggios and other tonal
puns, which are so numerous and ubiquitous that intention seems inevitable),
but they have been very suggestive to me as a composer.
This is why I continue to write [some of my] music serially or with other "arbitrary" or
"unnatural" systems or materials. Rather than trying to avoid octaves and tonal triads and
subconsciously internalized voice-leading rules-of-thumb, I do want to use those elements,
re-contextualized and juxtaposed in odd, bizarre, and unexpected ways that shed
new light on the objects themselves.
As a composer, then, I'm interested in systematic composition, like
serialism, but I'm not so interested in serialism as a language in and of
itself, but rather in using it as a fragmenter of the familiar. Likewise, to the person who asks,
"Well, if you want to use triads, why don't you just write tonal
music?"---again, the point is that I want exactly to "refer" to
tonal music from something
else.
Perhaps it's more complex than that: I think the best serial pieces from the past were written
with this state of mind going on, probably subconsciously---as it was
customarily dogmatically insisted that serialism was its own language---but
sub-consciously, the reason that the best of those pieces work well, is that the composers were thinking
this way--i.e., desperately trying to "fake" a familiar,
"cognitively correct" syntax in the midst of this other, artificial syntax that they were trying
to be true to. And that is the state
of mind, as a composer, that I want to be in as I write certain of my
pieces: I'm literally interested
in "pretending" that I believe in the purity and goodness of
artificial systems in and of themselves, but behind my own back, I'm sneaking in their usage as
fragmenters of the familiar.
What I am talking about is different from, say, the system recently
elucidated in a Perspectives of New Music article by Ciro Scotto,[22]
that attempts more of an official marriage between tonal syntax and
pitch-class-set composition.
Rather than a marriage, that forms an official system that successfully
integrates the artificial with the natural (i.e. tonal in this case)
compositional languages, I prefer
to throw the two together in their pure
states---and, metaphorically speaking, watch them fight, make love,
decorate the house, milk the cows,
and maybe enjoy an occasional ice cream cone together.
For a specific example, In Scotto's system, there are specific ways of
elaborating the basic underlying structures. To write a neghbor-note melodic configuration, there are
certain notes one selects to use as neighbors in a particular
case--extrapolated from the underlying structures themselves. These may or may not be "neighbors"
in the traditional sense (i.e. 200
or fewer cents away from the pitch being elaborated.) In my way of working, on the surface of the music, there are
what seem to be neighbors, arpeggiations, and any number of other familiar
formations--but these formations are not re-defined as in Scotto's system, but
are re-contextualized.
There
are many examples of fragmentation
of the familiar in serial music of the past. Some have been discussed extensively. For example, the fact that Stravinsky's
characteristic "sound" (which, in the area of harmony, relates to
such familiar objects as the diatonic and octatonic scales, poly-tonal
harmonies, and so forth) was retained through several changes of musical
language is widely discussed throughout the literature. For an example we turn to the
"Bransle Gay" of Agon,
in which the following curious chord appears:

This
beautifully misterioso sonority
could be heard as A-mixolydian, i.e. diatonic, but, perhaps because of a prominent C-Bb motive that occurs repeatedly,
earlier, and later, in the bassoon (i.e. the "bass line") in this
short movement, one might hear it as an octatonic subset.

Abraham
and Isaac is a most uncompromisingly
"atonal" work, making its way very flatly and ascetically through a
set of winding dissonant lines, voicing a sacred text. Suddenly, right at the moment where
God, in the nick of time, prevents Abraham from sacrificing his son (m.
173), an electrifying set of chords
knocks one out of one's seat:

The
"electricity" of this moment is due partly to the fact that these are
chords; loud, medium-high
register, secco chords, in the
strings, a textural formation rare up to this point in the work; but it is no doubt contributed to by
the fact that these chords are tonally reminiscent as well, as indicated in the
example.
In
Schoenberg's String Trio, we find
a more subtle example, where, to my ear, the voice-leading seems to very much
suggest a tonal V-I cadence, but it's realized in an incomplete, fractured way, with many of the key
leading tones left unresolved.

In
Sand, there are places where the
fragmentation of the familiar undoubtably happens unconsciously, or
accidentally. In some places it
was more or less intentional. Here
are two examples:
The
first is an explicit echo of a triadic progression. Sometimes I scan through an array partition, looking for
some pattern of notes that strikes my eye as something familiar that might be
made to "pop out" of the texture. So, in the following array segment:

I
noticed several triadic entities peeping out of the structure:
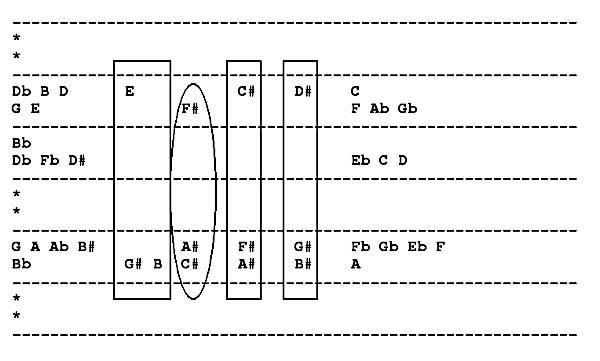
We
can hear this in Section 12 of the piece.
Another familiar
signifier I found on several occasions was the idea of a chain of
suspensions. In Section 25 these
manifest themselves as 2-3 suspensions (2-3 in the traditional sense of 2nd-3rd.) In another passage, (in Section
26) I find much
"narrower" suspensions:
minor 2nds (or augmented unisoni, the two being different intervals in
19tet) "resolving" to
major 2nds, and so on.
Indian
shenai-like (nasal-timbred) melodic passage-work briefly rears its head in
Sections 20 and 23.
These phenomena are
usually worked into the texture at hand---meaning that they are somehow related
to the default parser-unit---[02478t]12 in its various 19-tet interpretations, and their subsets.
Again,
"the familiar" is certainly not always "tonal music", or triads, but also phenomenon
like "parallel motion,"
or "suspensions", or "clusters" which need not be in a tonal context of any sort to retain
their significative power. In all
of the examples I've pointed out here, it has been fairly clear what, exactly,
was the familiar phenomenon being evoked, but there are many instances where a
passage may invoke a familiar sensation, but this reaction
may be quite complex and vague. . .we may not be able to figure out how it's
"familiar" to us.
I should also
point out that context is very important--more important than I have
implied. Some of the examples I've
presented here have been isolated from their contexts, and as such, they lose a
lot of expressive power. A V-I
cadence, especially a fragmented, impoverished one, is interesting in itself,
but in the context of the ending of the String Trio, it's an even more expressive gesture; the context
being both the atonal, harmonically ambiguous formations that lead into and out
of the excerpted passage; and the 12-tone structure, the motivic
structure---all of the aspects of the music that we ordinarily look into. I don't want to discount these latter,
but simply to assert that the things I have been discussing here are an essential
part of the musical experience, especially with this kind of music, and
therefore I choose to treat them with respect.
One might argue
that as a de-contextualizer of the familiar, random notes, or other algorithmic
schemes, could also work just as well as serial ones. I have, in fact, tried a variety of ways of disciplining
myself for these purposes, but I
find that I prefer serial methods. There are doubtless a number of
reasons for this that I'm not even aware of, but something I can articulate is that I like the way that
serial structures themselves can, on occasion, "pop out" quite
obviously onto the music's surface, in spite of themselves. They can, in short, "act at
various distances from the surface of a piece."[23]
This adds another layer of richness to a work.
II.vi.
conclusion
I like to feel
that I am working with these methods to get out of them something that they are
not--or something they would, at first glance, seem to be unlikely to
produce. The very idea that Berio
laughingly dismissed is the cornerstone of my composition aesthetic here.