I.
A composer's
response to flatness in musical form
I.i. Introduction
As a listener and
composer, I think often on the topic of musical form. I am interested in
exploring forms that challenge me as a listener. The music that I have found
consistently to be the most challenging and frustrating, yet also ultimately
rewarding, has been that that partakes of an aesthetic that we'll call flat
form. Music with a "flat surface" means
essentially: music that avoids
obvious or dimensionally conjunct large-scale goals, points of arrival,
"climaxes," sectional boundaries and the like. To the extent that these things do
happen, (sectional boundaries, climaxes, points of arrival, etc.) they happen only on a micro-scale. The music, and therefore often its composer,
intentionally thwart every attempt we make as listeners to parse it into larger
and [hierarchically] larger chunks.
The music that represents the flatform idea most vividly includes, especially, nearly all of the musical works of Milton Babbitt, but additionally, many works by other noted and un-noted late 20th-century composers. Prominent examples include John Cage (for example, certain performances of the Atlas Eclipticalis or Concert for Piano and Orchestra), Pierre Boulez (in the 2nd & 3rd piano sonatas), some works of Brian Ferneyhough (for example, the guitar pieces Kurze Schatten II), Iannis Xenakis, Charles Wuorinen, and many other composers.
I.ii. Flatness in Visual Art
The term "flat" draws an analogy between painting, the surface of certain canvases, and the surface of certain musics. Let us point the analogy specifically towards a particular one of the Abstract Expressionist painters, Jackson Pollock (he is perhaps the best example of what I'm talking about, though the ideas I'm discussing here certainly apply to works by other artists of the time (for example Willem De Kooning, Robert Rauschenberg, Frank Stella, and Joan Mitchell.)
The first time one looks at a Pollock painting, (one of his mature works), a certain state of shock and bewilderment in the face of the exuberant amounts of detail, may certainly be expected to occur. However, if the following example is encountered after viewing many Pollock works, especially in a context such as this one (reproduced in an essay, article or catalog), the experience may be far less electrifying:

Jackson Pollock: Number 5, 1948
There is no depth here, not much "stands out" or is "more important" than anything else, there is no "climactic point," or "center pole" or such on the surface. Nothing is important, because everything is important. On the one hand, one can see this as a complete lack of richness---just overall greyness. On the other hand, one could see this as remarkably rich: the picture is filled with tiny "sub-pictures", micro-pictures, anywhere you look. Zoom in on a 2" square anywhere on the painting, and you are rewarded with an interesting little structure, a powerful color combination, or a set of expressive gestures colliding in some interesting way. In such a local formation, we can find a hierarchy of importance in the details, a depth that the overall painting lacks.

Jackson Pollock: Number 5, 1948, detail.
In a museum or gallery, when the painting is hanging there in front of us, we can "zoom in" anywhere, at any time, and probably find some such local formation to think about, or one that arouses some sort of emotional or visceral reaction within us. We are able to make contact with the painting, and have a meaningful experience with it.
If the only way we could see these works was by looking through a catalog of reduced reproductions, we would be forced to regard these paintings from afar, always as wholes. Viewed thus, they are less interesting. From afar, they tend to lapse into dull greynesses. It's harder to make contact with them, to have a meaningful experience with them. To put this another way, there is no reduced, "Reader's Digest" version of the paintings. They are, in a sense, irreducible. If one is unable to zoom in on the detail, there's no point in looking at them. In a way, the artist has forced us to look at the detail, or not to look at all. If we try to walk away smugly, claiming to have "gotten the basic idea" or the "overall structure of the whole," our report of the "basic idea" is likely to be merely "a lot of zig-zagging drips, drops and chaos"; not a very interesting report.
The report that we would make on EXAMPLE 1.2 might be more interesting: "A big wobbly silver cross dominates the picture. This is crossed by a prominent yellow streak, moving from the upper left corner down beyond the middle right edge. . . " We could continue, talking about aspects of smaller incidental detail, and the way that the more important elements relate to the latter, and so forth. To get a "taste of" Pollock, (in a catalog, for example), it would be much more rewarding to pick a spot like this, and look at it zoomed-in, than to see a whole picture from afar, reduced.[1]
Let's look at a picture which, in terms of flatness, might be considered a complete opposite of the Pollock picture. This is Picasso's Woman With Pears:

Pablo Picasso, Woman With Pears, (Fernande). 1909.
This is obviously a much more hierarchical, (we might say "hilly", as opposed to flat) piece, than the Pollock. As our eyes move towards the center of the face, or towards the pears, the density of detail intensifies greatly. Our eyes are guided and directed to these spots. Thus there are, in a sense, "climaxes," there is a hierarchy of importance to the objects in the picture, one visible at some distance from it.
As I speak about these different approaches, it is important to note that it is not my goal to make any quality judgements here: both of these formal ways of working are valid, and both have their disadvantages and advantages. With the Pollock, we are free to find interesting detail anywhere we look, but it's up to us to zoom in somewhere; with our freedom comes responsibility and effort. With the Picasso, our task is easier, but less free: Picasso guides us to the most detailed parts of the picture, but he tells us where they are; he tells us what to contemplate.
On the other hand, the Pollock cannot be reduced into a catalog, and therefore cannot be distributed widely, beyond the museum, as successfully as the Picasso. I feel that most of what Woman with Pears "is" can be seen in a color reproduction. Although I appreciate the chance to see the real painting, I am quite happy looking at reproductions.[2] The same is not as true of Pollock pictures.
We might imagine that these two pieces are on a line or a continuity, measuring many different possibilities between extreme flatness, and extreme "hilliness", on which one could locate works of art. There are many works by Willem De Kooning, for example, that are teeming with detail, but are not completely flat in their overall structure. We could probably say or feel some interesting things about the "whole structure" of the following reduced De Kooning picture; there are interesting local areas worth exploring as well:

Willem De Kooning, Untitled V, 1980
For the moment, however, I am concerned with the extremes of "flat surface", and the question, "Is there a way for the observer to make make contact with a work that exists at this extreme?"
In the case of visual art, most people probably wouldn't quibble with an answer in the affirmative. In music, however, it is less clear.
I.iii. Flatness in Music
Let us extend the flat analogy to music. What is non-flat music? The golden example of a "perfect shape," taught widely throughout the musical academy,[3] is the first movement of Bartok's Music for Strings, Percussion and Celesta, with its perfect arch. This piece is in what we might call a "single mountain" form.
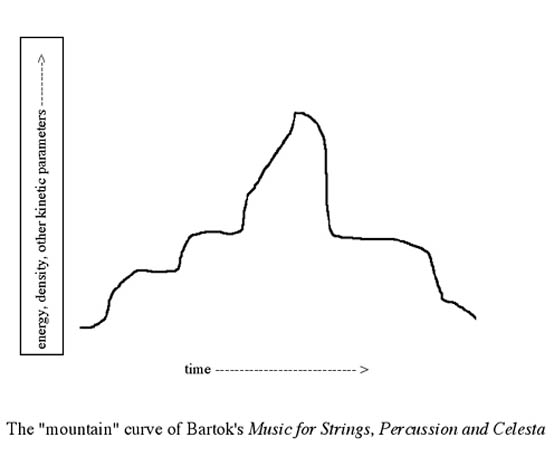
We know, or can easily imagine composing, works that are more complex, in terms of "climax" points and other energy-over-time considerations: for example, hilly terrain of various kinds are what usually characterize a typical Mahler symphony movement:

A typical Mahler symphony's "hilly" kinetic curve
Perhaps the following energy-scheme reminds us of the Pollock:
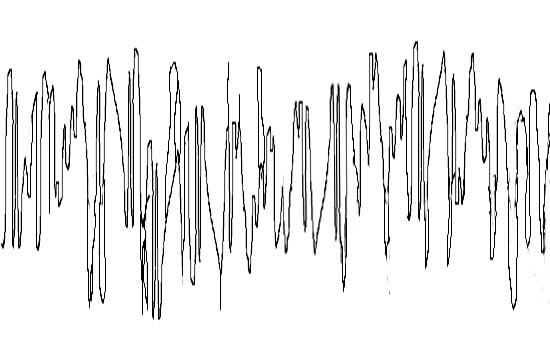
Kinetic curve for a "flat" piece.
This is a kinetic curve for a piece of music that we might say has a "flat surface." Again, in terms of whatever parameters are important to our determination of kinetic--or other--forms, there is a lack of hierarchy at all but the most local levels. Nothing "stands out" or is "climactic" or is "more important".
What is it that we're measuring with these curves? There are many musical parameters that could be telling us a section is "important" or "climactic"----loudness and register are only the most obvious. Others include density, overall level of dissonance or tension, harmonic rhythm, tempo---and a host of hybrid pitch/rhythmic parameters.[4]
In flat music, all or most of these parameters are constantly fluctuating from high to low, and they are not in sync with each other: There is nearly always a parameter contradicting the highs or lows of another parameter.
With a piece like the Bartok, I, as listener,
could perform the rather violent act of playing a recording in the following
manner: play 2 or 3 seconds of
music, fast-forward 10 or 20 seconds, repeat until the piece ends. At the end of that, a listener would
probably still get the "basic idea" of the form of the piece---there
is a carefully worked-out and worked-toward climax. Using the same procedure on a flat piece, the "basic
idea" would only come out to "lots of random ups and
downs." To be able to
say only that, after hearing a piece, doesn't speak of having had a very interesting listening
experience with it. But if we "zoom in" on the music,
we might find, as we did with the Pollock, lots of interesting, quirky, bizarre
or unexpected events or micro-sequences of events, all worth exploring.
"Mountainous" music, like the Bartok example, or any of the movements of Sibelius' 5th Symphony, (another example), is often tremendously satisfying. But, it is possible with those pieces to enjoy the music without really listening to it, to let it "wash over" you. The first movement of Music for Strings, Percussion, and Celesta, is teeming with detail, but it's not absolutely necessary to follow that detail to make some kind of contact with the piece.
With a flat piece, the inability to engage in the "wash" experience is both a strength and a weakness. In one sense, it empowers us as listeners, in the same way that we are empowered walking through a museum, able to view any work of art from any perspective, or any combination or sequence of perspectives, and able to make our own decision, (or no decision at all), about what details are more or less important.
As Robert Morris put it: "A piece of music is like a public park or a garden where one puts a lot of energy into the design of the thing to make it interesting...there are fountains and hedges and there are gardeners who take care of the flowers and there are some wild parts and some places that are very civilized where food is served. You know, you work all of this out...but when a person goes into this space, he or she doesn't have to visit its parts in any particular order...the piece is waiting for the listener to explore it."[5]
However, for all that I enjoy the micro-level richness of the forms of these works, this music also frustrates me. Any given moment in a flatwork by Ferneyhough, Babbitt, or Boulez I usually find to be elegant, exquisite, violent, expressive and/or interesting, often in some bizarre way. But the intense compression, the density in time, of all of these exquisite, individuated moments tends to negate their individuality; as a listener, my ability to account for each event's individual character, as well as its relation to its immediate surroundings, is dulled quickly. In the best of situations, I am able to "zone out" for a while, and then "tune back in" at a later time, but only to catch a few more events, out of thousands, each of which deserves my full attention.
The problem with flat music is thus similar to the one that a Pollock picture has when it's presented in a standard exhibition catalog: all you see are the grey whole art-works, and there's no way or opportunity for you to "zoom in." Most people's experience with flat music is analogous to this situation. This is the experience one gets hearing a work all the way through in a concert hall, or listening to a track on a CD.
These problems have
been discussed fairly extensively, by composers ranging from from Xenakis[6]
and Smith Brindle,[7] to Lerdahl,[8]
in a variety of ways. These
writers most often take the view that because flatforms lack an overall arch or
a sense of an overall hierarchical formal design, they tend to fail. My frustrations are somewhat different:
I do not feel the need for an overall formal arch, or hierarchical structure; I
like heterarchy and anarchy. What
frustrates me about flatforms is simply the fact that the high density of
events makes it impossible for me to give each event the perceptual attention
it deserves, as an individuated human creation. Xenakis, Smith Brindle, or
Lerdahl might argue that the speed of the events in a Babbitt piece, generally
speaking, calls for a decrease in the emphasis on the individual events
themselves, and more emphasis on the events' participation in an accretive,
tension-building form. These
writers have, for the most part, taken a rejectionary stance, regarding
flatform as a dead-end of 20th-century compositional experimentation, and not
worth pursuing compositionally any further. I have been tempted to make this rejection as well, at
times. Yet, I feel that outright
rejection is too simplistic a solution to the problems that this music
presents---because, after all, this music also presents us with many musical
treasures: vivid, individuated, sonic moments and their local relations. Instead of rejection, I am drawn to
thinking through alternative ways of both approaching this music as a listener,
and presenting it as composer or hypothetical performer/presenter.
Through my experiences
as a listener I tried various approaches to come to terms with this music.
Naturally, due to most of the writing on the music, one's first attempt to get
to know it inevitably involves investigating the question of whether repeated
listenings will eventually put one in touch with the underlying structure (i.e.
12-tone structure in most cases) of the work. This is, no doubt, possible for
some works, but only if one "trains" oneself to hear these things, which
would require a score, as well as foreknowledge of the technical procedures
involved. However, as a rule, I want to come to terms with any music
in a way that requires only that I listen to it and draw conclusions from my
perceptions. I never look at the scores of works until I've made meaningful
contact with them as a listener first.
I am looking for aspects of musical structure that come out through
listening only---and these compositional-grammatical structural features don't
present themselves on the surface nearly as often enough as they would have to
for that to happen.[9]
For a while, I thought
that this music (flat music of the late 20th-century) might be
accessible through memorization (memorization as a listener, not a
performer): through memorization,
a listener could eventually follow and anticipate every gesture, melodic
movement, and harmonic affect, during
the listening experience. I think
"anticipation" is a major factor in what makes the
"learning" (memorization) of music (again, as a listener) something
that human beings find worthwhile. A kind of pleasurable "click"
happens in the mind, a sort of release occurs, when we encounter something we
have been anticipating. Thus, I thought
memorization could be a way of making meaningful contact with the musical
surface.
With a 15-minute work
whose musical surface is organized hierarchically on the large scale (such as a
movement of a Mahler symphony), most listeners can attain a more or less
complete "anticipatory" experience (i.e. the whole work is gesturally
"memorized") with relatively few repeated listenings. This is not
very difficult, and can indeed result in some ecstatic listening
experiences. I remember that, with a youthful mind, fresh and
empty, it took me but a week or
two, and a handful of listening experiences, to memorize the 2nd and
4th symphonies of Mahler, to a high degree of detail. As I "air-conducted" these
pieces, I knew every cue. Although
the number of people who spend their adolescence "air-conducting"
Mahler symphonies is low---it is not completely negligible: I have, in fact, met many. They've had similarly easy times
memorizing the surfaces of these works.
To memorize an entire
15-minute long Babbitt work, or even a set of miniatures such as the Kurze
Schatten of Ferneyhough, is impossible,
after only a handful of listenings.
Performers of this music, or those with access to the scores, or other
methods of achieving the redundancy necessary for the memorization process, are
able to do it, but again, I was searching for a process that would be available
to any willing listener, (regardless of their music-technical skills), who
would put in the same amount of repeated listenings that, say, a typical
pop-song is often given.
So this idea of trying
to "know" or "master" the work through memorization and
osmosis was apparently not going to lead to a solution to the frustrations of
flatmusic.
I have been told by
several instructors of Columbia University's Music Humanities course (music
appreciation), that students seem to be generally partial to Webern (such as
the Op.9 Bagatelles for string
quartet), but dislike Babbitt and Cage.
From the point of view of these students, most of them non-musicians,
I'm sure these were very similar musical languages. The ear hears gestures,
non-tonal (often dissonant and unfamiliar) and non-pulsed, and therefore
completely "random" from the point of view of the typical
music-humanities student; in the
Webern, however, there is space between the gestures, and then between the movements--time
for the listener to ask him/herself,
"What if that random stuff were actually music? How would I think
of it as music?" They have
time to make associations, however distant they may be, with various sonic
experiences they've had or are familiar with, with images that may come to
mind, emotional affects and
implications, and so on. In short, they have time to "get to know"
and "learn" the musical gestures.
Eventually, I hit upon an idea: given a longish flatform work, I would pick out an arbitrary segment of the music, of no more than a minute in length, loop that segment, and see what micro-listening experience I could get out of it. I would choose some time frame on the CD recording, for example 5:11-5:45, and listen to it 7 or 8 times in a row. I would "get to know", in both visceral and felt, as well as intellectual and analyzed senses, the passage: its gestures, events, harmonic character, local pitch relations and repetitions, motivic content---whatever presented itself.
This may not seem like a particularly revelatory idea: after all, if I am a theorist preparing to write a paper on a given work, this kind of "focussed-in" listening to a certain passage would be essential. However, it is not generally regarded as a "natural" way of listening to music, but rather a way of listening one engages in only when one is doing scholarly research and investigation. For most musics, this state of affairs (where "zoomed-in" listening is reserved for "experts only") is perhaps regrettable, but not destructive; "lay" listeners, encountering the whole work a few times, begin to build that anticipatory memorized "skeleton" of the work; future listenings to the entire work will gradually fill in aspects of the details of the work necessary to build towards richer and richer "anticipatory" experiences. With flatmusic, however, this memorization is far more difficult, as there is no hierarchical structure on which to "attach the details" necessary for the anticipatory experience, and thus the usual paradigm of repeated listenings to the whole work will likely be unsuccessful.
But the result of my experiment with
"zoomed-in" listening was revelatory: pieces that had seemed
intolerably dull, too dense, and too flat, suddenly began to open up to
me. Enjoyable listening
experiences---from the sheer sensual joys of encountering
musical objects consisting of varied timbral, harmonic, linear, and rhythmic
formations (or, most often, hybrids of these aspects), to making any number of
quite simple local music-structural associations--became available for
experiencing in the context of works in flatform.
It might be argued,
"Why not take these beautiful moments and stick them into a more
immediately satisfying hierarchical situation? Then you get the best of both
worlds: beautifully detailed local formations; and an overall form that's
easily swallowable. . . "
The first of my own answers to this question relates to a recent trip to Venice, where I was confronted with the Basilica of St Mark. This vast edifice exactly fits the description of a form just given. The underlying structure is relatively simple in its overall design. Over the centuries this structure has become more and more encrusted with details: what started out as a building in brick, was covered first in marble (each block of which presents, on its surface, a detailed and unique pattern of swirls and shapes of various tints); then, over the centuries, more and more elaborate decorations were added: capitals and wall carvings, elaborate roof statues; mosaics that covered the lunettes, the inner walls, ceilings, and floors; decorations and restorations up until the present day. Still, the underlying structure quite clearly remains to guide the eye, and to structure the detail.[10]
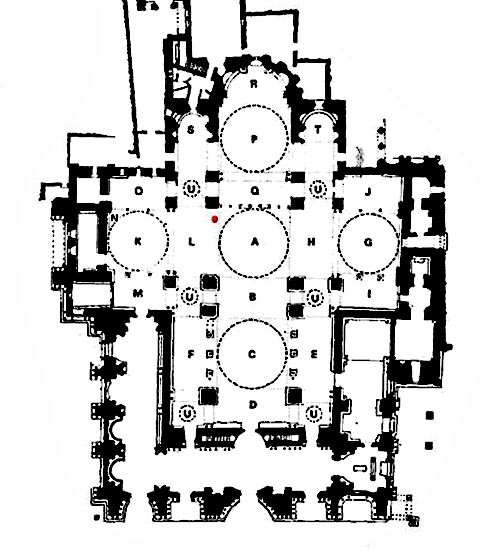
Basic form-plan, Basilica of St. Marks, Venice.
The way the detail "encrusts" a basic overall design is analogous to some of Pollock’s early work, for example, the She-Wolf. Though mesmerized by the massive detail, I felt immediately that I would be uncomfortable working this way compositionally. I feel far more drawn to the opposite, where simple structures seem to arise from dis-organized, anarchic, teeming detail.
There are political ramifications we might consider as well. Although serial, and therefore, often flat music is accused of being the political analog of fascism, we can turn that argument around: it is quite possible to see the former way of working as hierarchical, quasi-fascistic in its implications: any detail is immediately assimilated into a pre-ordained hierarchy. It (the detail in question) has, in effect, no “say” in how and where it goes into the basic structure, or in the form of the basic structure itself. (In the case of the Basilica, there are even darker political implications, as many of the "details" are items brutally sacked from various Middle Eastern locales, especially Constantinople.) On the other hand, the latter way of working is about small, self-organizing “collectives” of details, where individuals see how they might relate to one another, and then strengthen those found connections, forming tight local structures, while still maintaining their own identity. Thus the entire structure is tighter and stronger because its connections are so intricate and unpredictable: there are no details that "dominate" the structure, whose loss would bring it toppling to its destruction. We can relate this to contemporary methodologies of progressive social change.[11]
The second answer to
the question is that a composer working in flatform wants to disallow their
work to be reduceable, "journalistically," so to speak. I spoke earlier of there being no
"Reader's Digest" version of
a piece. There are works, even
great, detailed ones, that can be described in such a manner. The first movement of Sibelius' Symphony
#5
is a masterfully done climaxform, also highly detailed; yet it is possible, even probable, that
a listener, satisfied by the grand working-out of the climaxform, may find no
compelling reason to look deeper into the details of the piece. Surely there is something sad about
this, about the fact that someone can make a tidy, "sound-bite"
description of a piece, and leave their acquaintanceship with the music at
that. By making a flatform, one's
goal is that the only way that someone
can approach the music, is by listening to the details. If they don't pursue the latter, they will get nothing
out of the music.
Plus, a great amount of
the interest/charm of the individuated moments comes from the very fact that
they are not associated with a musical
hierarchy, the fact that they appear almost randomly---to give them a
"reason" for existence or instantiation at a given point, via a
hierarchical structure, robs them of much of their inherent character.
What composers such as Babbitt, Wuorinen and Martino largely ignored was the issue of presentation---of placing the music in the best possible listening paradigm. It occured to me then, as a composer who was interested in making flat pieces, that the "zooming" exploration of the music I had discovered had to somehow be a part of the piece itself. One way of making that happen would be to put a lot of space in my music, or lots of repetition of the individuated events and their local relationships. This is, to a large extent, the solution employed by Morton Feldman: in his music, there's always lots of room to think about what's just been heard before the next event overtakes it.
Alternatively, I could go for a kind of breathless, exciting, maximum density of events, but have the piece come with its own interface that would allow the listener to, as with the Pollock, "zoom in" on the work, check out its little 2" squares, its little micro-structures and micro-moments. In other words, the listener would be free to choose their own perspective on the work.
I decided to extend the idea: not only would such an interface allow "zooming" in the time domain, but it would also allow for "architectural exploration" of the work on all sorts of levels of counterpoint.
I.iv. The Interface
The interface is shown in the following example:

The Interface.
Its workings are fairly straightforward: Time is measured in measures and beats, with 19 beats to the measure.[12] A timeline of the music in the current section of the piece is found at the bottom of the display. Ideally, I would have wanted to have the entire piece available for perusal via this one time-line, however, for technical reasons, the piece must be digested in Sections of 6-10 bars each. Thus, clicking somewhere on the timeline starts the music playing somewhen in the current Section. Unless one clicks the timeline again somewhere, the music will eventually reach the end of the current Section, and flow on into the next Section. This can go on indefinitely, thus allowing the piece to be listened through as a whole.[13] Clicking and dragging on an area of the timeline sets up a loop, and while the selected passage loops,[14] contrapuntal exploration of the work may be engaged.
The counterpoint is multiplexed in a number of ways, usually by groups of six: thus there are 6 (pitch) registers, 6 stereo positions, and 6 loudness levels. Each of these is referenced by a red [virtual] button which, when off, will prevent any notes with that characteristic from being played. Hence, turning off the 3 highest register buttons will result in only low-ish or medium-low-ish sounds. There are also buttons for the different instruments: wave, filter, piano and concrete; buttons for turning on/off spatialized and/or unspatialized notes, and so on.[15]
There are also volume sliders for many of these parameters, allowing for a more subtle variation of the texture. This reflects the fact that, at its heart, this is a "live-mixing" paradigm.
I.v. Basic Aspects of the Inner Workings of the Interface
The interface was constructed with the MAX/MSP package.
To be able to mix and remix the notes of the piece in so many ways, it is necessary that each note be stored as a separate sound. Because of the huge amounts of computer memory necessary for this, not all of the notes of the work can be accessible at one time, and the piece must be broken down into sections. For each section, all of the separate note-sounds are collected together into one soundfile, eventually loaded into a buffer~ object in MAX/MSP. These buffer files are huge, sometimes on the order of 40 megabytes of 44.1K stereo sound. A separate text file, whose eventual destination is a MAX coll object, contains data about each note stored in a given buffer~.

Part of a MAX coll list containing data about note-sounds in a particular
buffer~.
I will not go into a minutely detailed explanation of the workings of the interface. The basic procedure is as follows: a given section's buffer~ and coll are loaded into memory. As the music begins to play, clock-times and note-data lines in the coll, ordered sequentially, are pushed through several decision-networks.
These ask questions, all of which must be answered in the affirmative for the note to be played:
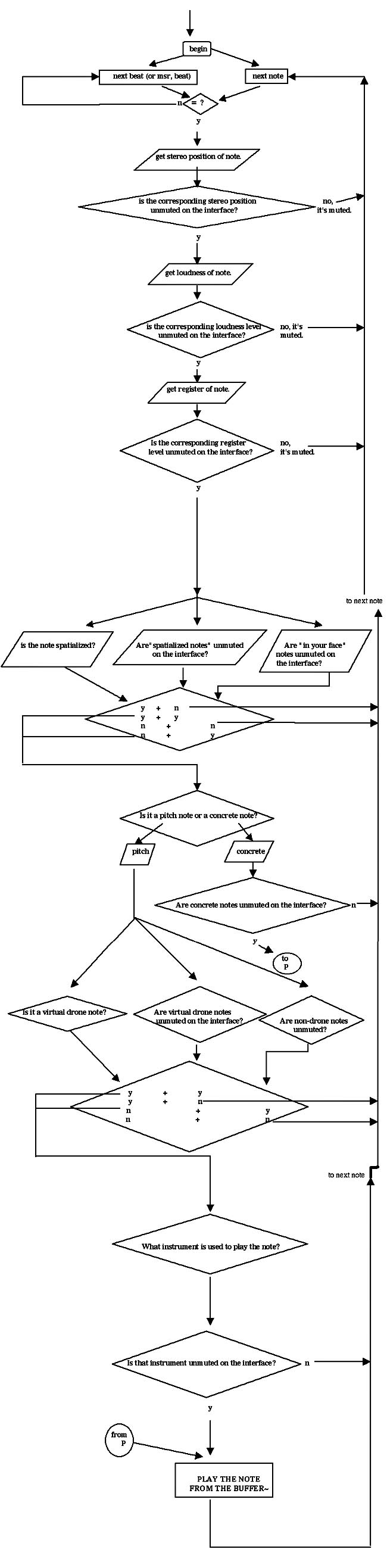
Flowchart of the workings of the MAX/MSP interface.
Additional procedures are developed for when the music has come to the end of a loop, and must loop back, when it's come to the end of a section, and must flow on to the next section, and for making sure the volume sliders have their appropriate effects.
I.vi. Towards a More Concrete Definition of
Flatness[16]
I will now attempt to define, somewhat more formally, what I mean by "flat" in the domain of music. How "flat" a piece is, is a subjective issue, varying from listener to listener, also varying depending on how familiar one is with a work, aspects of a particular performance, one's mood during a given listening, and a host of other factors. Therefore, instead of advancing some measure that will provide a definite value or yes-or-no answer to the question of the flatness of a work, I will simply propose some pseudo-measures and methodologies, and highlight some musical aspects and categories that might aid one in discussing or defending one's own subjective opinion on the matter, as it relates to a given piece or passage. One important point is that flatness is not simply a measure of density: a highly dense work such as La Chute d'Icare of Brian Ferneyhough is not, I feel, a flat piece. I hope the preliminarily hypothesized tools outlined below might help me to explain why I feel that way.
Flatness means a piece is problematic for the listener. It is difficult to enjoy, to "get through," to make contact with. Why? Paradoxically, it is because we can't ignore it, we can't "tune in and out", while still more or less keeping track of the music. This is because of two kinds of factors: we can't detect lines of large-scale motion in musical parameters (loudness, pitch register, etc.), that allow us to tune out and then back in, and still know where we are, more or less, in the progress of the piece--this factor we'll call kinetic curvature; or, we can't chunk it on a large enough scale, so that if we tune out and then back in, we still know which chunk, (or, hierarchically speaking, chunk of chunks) we're in--this factor we'll call sectionalization; or, a combination of both of these problems.
I am assuming a listening situation where a listener is giving (or trying to give) a piece their full, undivided attention. Using a piece as ambient background is thus not an example of such an experience. I am talking about listening to an entire piece, from beginning to end.
I should also note that the passage or piece of music needs to be fairly long, at least 1 minute or so. Otherwise, the concept of flatness is more or less irrelevant. In other words, below a certain minimum length, almost any piece is "hilly," (the opposite of "flat," especially in terms of kinetic curvature) or chunkable. Above this minimum duration, flatness will always be relative to unit time, not to the scale of a piece. The kinetic structure of an entire act of a Wagner opera, or a movement of a Mahler symphony, may seem, compared to the whole piece, quite flat (lots of ups and downs. . . climaxes and climinses); however, per unit time, it's still quite hilly--there is enough time between the ups and downs of the music to be able to keep track of it--at least locally.
I.vi.2. Kinetic
Curvature
Kinetic curvature is the measure of flatness that we've been (if sometimes implicitly) using for most of this Essay so far. Put simply, this involves taking measurable musical parameters, making graphs of their values over the course of a piece, and then simplifying those graphs and determining therefrom how "hilly" the piece is. There will be a number of measurable musical parameters for a given passage or piece, so to determine the "degree of flatness" of the given passage, in terms of its kinetic curvature, we need to calculate the combined and cumulative effects of all of the parametric curves.
The entire procedure can be written out algorithmically as follows:
1) Select 2 or more of the most salient musical parameters necessary to characterize the passage. (If we are comparing 2 or more musical works, we will need to use the same number of parameters for all of the works.)
2) Plot their graphs over the course of the passage.
3) Next, the graphs need to be simplified to within a certain degree of complexity. What this means is that, for a given unit of time X, we need to "low-pass filter" the graph, (average it out), so that it contains a maximum of N swoops, or direction changes, per unit time X (these values would need to be determined empirically, through experimentation, but my intuition at present is that beyond 1 or 2 ascents/descents of a parameter's value, per 1 minute of time, the ascents/descents become local detail rather than large-scale motion---and hence, should be "filtered out" of the curve.)
4) One inspects these results for all graphs. For each parameter, a meaningful indicator of "tolerance" has to be determined, to measure whether a given graph is more or less flat, or not. This tolerance would be the same regardless of the length of time of the spanned music. Thus, the level of fluctuations in a graph fluctuating between mp and mf loudnesses, for example, would not be very meaningful on a local level; nor are they on a global level. If the graph stays within this "tolerance" level of fluctuation, it is then further filtered to flatness. We can liken this step to removing any smaller "hills" and retaining only larger "mountainous" moves.
5) We produce a measure of HILLINESS of each graph. We might provisionally calculate this as the number of directional changes in the graph (we've already skimmed off any small hills, so any direction changes indicate large hills or mountains. We've also filtered out very rapid ascents and descents, so these hills or mountains will take up a lot of time as well).
6) We sort the HILLINESS parameters, for all of the parameter-graphs, from high to low. We then take an average that is weighted very much towards the highest HILLINESS value. This reflects the intuition that just one high HILLINESS value goes a long way towards unflattening a piece. Additional high values help or hinder the value, but in decreasing amounts as we go down the list. This gives us a single, overall, HILLINESS value for the piece.
For an example, imagine a piece where all parameters are fluctuating wildly at all times (or alternatively, not fluctuating at all), giving HILLINESS values of 0, except for one parameter, say, register, which describes a very clear mountain-curve from low to high and then back, or the like (a HILLINESS of 3 or 4 total for a piece, let's say). The ear would be able to grasp onto register, and would have a lot less difficulty parsing the piece than if register were also fluctuating wildly.
7) Finally, to account for the cumulative effect of all of these parameters, we can modify the total HILLINESS of the given passage/piece by adding a function called CONFLUENCE. This would reflect the intuition that several graphs moving "in sync" would push the HILLINESS of a piece way up. Hence, with a work like Music for Strings, Percussion and Celesta , 1st movement, the fact that many musical parameters (loudness, textural thickness, registral outline, etc.) are moving in sync in simple mountain curves, greatly increases our perception of the piece as one big mountain-form. Function CONFLUENCE is as follows:
LOOP: FOR G1=each graph
LOOP: FOR G2=each other graph that hasn't been a G1
already.
LOOP: FOR DC=each direction change in G1
QUERY: is G2 in the same place at this point
in time, changing direction in the
same way?
YES-- HILLINESS= HILLINESS+1
NO -- go on
NEXT DC
NEXT G2
NEXT G1
Thus, the procedure basically counts the number of "in-sync" moves between graphs, and adds these to the HILLINESS parameter. Thus we get a final value for HILLINESS.
Here are two examples of what might come out of the procedures described above: one, for what I think of as a very "flat" piece by Babbitt, and another for a quite "hilly" work, by Varése. I emphasize "might" because for several of the procedures and measures (e.g. the "low-pass filtering" and the "weighted average"), I have not determined the exact calculus that would produce the most useful and intuitive results. Therefore the following Example can be viewed as a kind of prototype:
Flatness analysis of Babbitt, Around the Horn, mm 1-50, and
Varese, Density 21.5 :
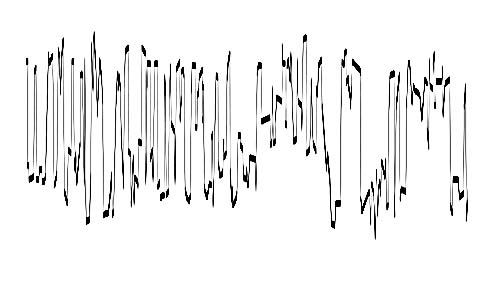
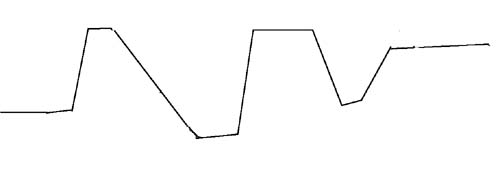
curve of pitch movement for Babbitt, Around the Horn, mm. 1-50

Same curve, low-pass filtered.
HILLINESS=(app)=5
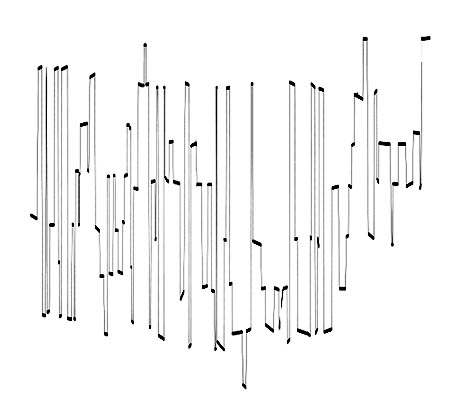
curve of loudness levels for Babbitt, Around the Horn, mm. 1-50.
Curve of pitch movement for Varese, Density 21.5
"low-pass" filtered curve of pitch movement
Curve of loudness movement for Varese, Density 21.5
"low-pass" filtered curve of loudness movement
I.vi.3.
Sectionalization: The
"sectionalization" of a piece is a measure of, for a given work, the
mind’s ability to “chunk” the music into discrete parts, and
to keep track of a hierarchical organization of these chunks. This
is related to "grouping structure" in Lerdahl and Jackendoff's A
Generative Theory of Tonal Music.[17] There are three aspects of
sectionalization that we consider in regard to the flatness of a work. The first aspect, regarding depth, will be the primary
aspect. The other two aspects,
regarding absolute temporal length of groups, and differentiation between
groups, affect the power of the first aspect in determining a work's flatness. Flatness, as one might imagine, is strongly
affected by the depth of grouping structure. The less possible it is for the mind to meaningfully
assemble smaller groups into larger and hierarchically larger groups, the
flatter the music is likely to seem. The highest level of grouping structure is always
the whole piece. As the level of
grouping structure directly below this
top level, and the lowest level
of grouping structure approach each other in the grouping hierarchy, (i.e. the
fewer the intervening levels), the music becomes flatter and more difficult to
parse, or at least to keep up with.
Near-flatness caused by lack of hierarchical depth In considering the second aspect of of
sectionalization, absolute temporal length of groups, if the groups on the lowest level of grouping structure
become too long, the music within those sections becomes difficult to
parse. This can happen in music
where individuated events and textures or textural movements are difficult to
hear. It's actually quite
difficult to find relatively event-less music. One might think of Schoenberg's Farben, or Ligeti's Atmospheres, but both of these works have clear sections, moments
when new textural elements break into the discourse subito and thus, they contain the impetus to divide the
surface up into grouping structure.
Perhaps Morton Feldman's For Samuel Beckett is a good example of near-total-smoothness. A "shallow" grouping
structure--indicating a tendency towards flatness--might yet be un-flattened by
the following effect: there is a
level of groups wherein all the group sizes are roughly even, and their
time-lengths fall between 15"-45" in length. This is the period of time during which
the mind is still excited about a new section having begun, but not yet
"bored" or "zoned-out" from the new material. Sections of this duration are just the right length to allow the mind to
follow the music, section by section, despite possible lack of hierarchical
organization. Many works by Morton
Feldman, for example For Philip Guston or
Crippled Symmetry, manage to escape the pitfalls of
flatness in this way. The final aspect of sectionalization is a measure
of differentiation between the sections.
How well are they contrasted?
One can measure this in a crude way by counting the number of parameters
of the music that change in relatively drastic ways. Thus, if soft music with consonant harmonies for strings
suddenly gives way to loud, dissonant brass textures, then the differentiation
has been accomplished in 3 ways. For an example of dealing with these 3 aspects of
sectionalization, consider Milton Babbitt's Whirled Series for saxophone and piano. The first 3 sections of the work begin at approximately
0", 25" and 45".[18] These sections are usually defined only
by the fact that different registers of the two instruments come in and out of
play. All other elements of the
texture remain more or less constant (meaning they'd be flat on a
filtered-graph of kinetic curvature).
This sectional rhythm remains more or less the same for the entirety of
the 16' work. The grouping structure is shallow (in many ways
it ends at the level of the 25"-long section: the next level up is the whole piece); and although these 25" sections
are just the right length to defy flatness, nonetheless, the differentiation
between the sections is quite low (only 1 aspect, more or less), (the first few
times I listened to this piece, I missed the sectional aspects entirely). So for many listeners, especially
on the first few hearings, the piece is effectively flat. For a listener highly familiar with the
work, the sectionalization may assist in un-flattening it to a certain degree. I.vi.4.
Conclusion As
I said at the beginning of this discussion, my purpose here was not to present
algorithms that will return a "yes it's flat" or "no it's
hilly" answer, or even a numerical designation of flatness (a location on
the curvature/sectionalization plane). Those answers may vary from performance to performance, and
listener to listener. What I set
out to do was present some tools to discuss our intuitions, so that we might
have meaningful dialogues with one another about these issues.
result of "low-pass filter"---no global dynamic movement.
HILLINESS=0
weighted average of pitch and loudness: HIlLLINESS=(app)=3
total HILLINESS after CONFLUENCE procedure=(app)=3

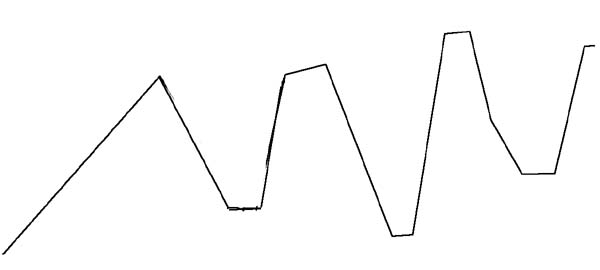
HILLINESS=(appr)=7
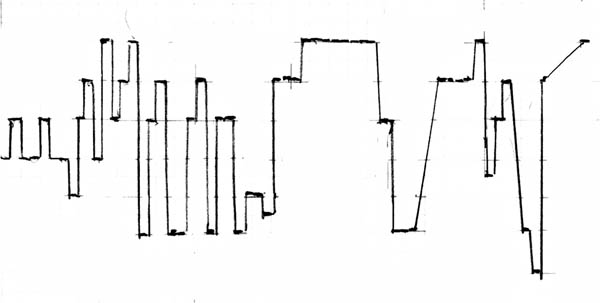
HILLINESS=(appr)=6
weighted average of pitch and loudness HILLINESS: 7
CONFLUENCE: 5 synchronous directional changes
total HILLINESS after CONFLUENCE=7+5=12

(no musical criteria for deeper hierarchization of lowest level)