III
The Virtual Instruments of Sand
III.i. Introduction
The final topic I will address involves the most small-scale and atomic levels of the piece, those of the actual sounds used in creating the work.
Like many composers of instrumental music that move into the computer-music realm, I often think of music in terms of pitch and gestural structures most appropriate for instrument-wielding performers. My initial gut inclination is to find some way to transpose this kind of thought to a computer-music context. When a computer-music composer receives a comment like "computer-music is all just too ambient" or "you’re merely playing with sounds, this isn’t music yet" etc., these comments are coming from someone who, in all probability, wants to hear instrumental-type music (its gestures, harmonic and melodic structures) being made by the computer.
The problem with this is, as anyone who tries to effect this transplantation of compositional aesthetic realizes very quickly, that instrumental, gestural music, with its detailed pitch, harmonic and rhythmic structures, is not so easy to realize with computer-music tools. One can do it fairly easily with MIDI tools, but anyone who's heard a piece that engages this solution is aware of the sonic aesthetic limitations of MIDI. Common samplers and synths were designed in emulation of, and are therefore a cheap imitation of, actual acoustic instruments. On the other hand, what is relatively easy to do on a computer, and what sounds quite good on the surface of a piece of computer-music, is to dissect, examine, process, and re-contextualize real-world recorded sounds. Such sounds are often complex: harmonies or even [melody] lines might exist within these sounds, but these are usually mixed with noise and other kinds of inharmonicity, and all of this mish-mashing appears in such complex, ad hoc ways that to work such sound sources (samples) into the kind of complex pitch-structures that one might conceive of for string quartet, for example, becomes nearly impossible. Therefore, many computer-music composers often opt to let things be and try to structure their works in a more intuitive, perhaps seemingly simpler fashion. Although a growing number of listeners find this latter approach capable of producing interesting, expressive and complex (though complex in a different way from the way a finely wrought string quartet is complex) music, it is this latter approach that often seems to receive the "you're just playing with sounds" type of complaint.
While realizing gestural, densely-pitch-structured music on the computer is difficult, it is not impossible. (Ditto for producing good music with MIDI tools, as Bjork, the Freight Elevator Quartet, Amon Tobin, Sufjan Stevens, and a host of other superb artists working in the techno and related musical worlds have shown us.) I have attempted it here in Sand.
When I started this project, I was aiming to create a virtual (software-based) instrument that could be a totally neutral carrier of pitch, rhythmic, loudness and harmonic-gestural information. Ultimately, such a neutral instrument does not exist. Even in the instrumental domain, t his is the case. At first glance, it might seem that if one is setting out to write some kind of total serialized work, even for acoustic instruments, one might shop about for instruments that are as neutral as possible, with an even timbre over multiple registers, possibilities of all degrees of loudness in all registers, and so on. There are obvious candidates to reject (oboe, bassoon) and some that might suggest themselves positively: clarinet and piano (two instruments of choice, in fact, for serial composers). But, in fact, no instrument is neutral--The clarinet has its weak registers, the piano can’t hold tones indefinitely.
This is not tragic, however. In fact, it may be cause for celebration: it’s a matter of how we’re thinking about making music. For myself, what makes working with total serialization interesting is that I've got these materials that I've somehow got to get together to make some cool music. Besides some less than intuitively suggestive combination of loudnesses, rhythm, and pitches in unexpected registers, I’ve got to deal with a given recalcitrant instrument, or combination of instruments, which may have constraints like "I can't play loud in this register" or "my mf equals that other instrument's p" or "I can't do sharp attacks." Working within these constraints to produce viable music is a far more interesting and rewarding compositional process than working in some anonymously perfect neutral space.
Therefore, for this piece, I began by constructing a set of software instruments. However they ended up working, I would figure out how to compose music that sounded good on them--that would provide a context in which they would be musically effective. In other words, I would learn to "orchestrate" effectively for my ensemble. Thus, throughout the composing process, I have been steadily "learning to play," so to speak, this combination of virtual-instruments I've created.
There are four of them: Wwave, a dynamically-changing wavetable instrument, piano, a sampled piano instrument, filter, an instrument using a number of standard filtered-noise engines, and finally concrete, a musique-concrete gestural "engine." I will talk briefly about the first three instruments, and then somewhat more extensively about the last, which I think certainly leaves room for use in musical works in the future.
III.ii. Filter
Filter is a fairly straightforward instrument – its sounds are made simply, by various standard filter-types: elliptical, infinite-impulse-response, etc.[1] I’ll use it, however, to introduce the way in which these instruments are "scored" for in the piece.
When we write a score for an acoustic instrument, a lot of information, even in highly detailed scores, is left unsaid. That is, we assume that players will interpret certain symbols by producing a complex series of actions on their instruments, resulting in a complex series of sounds. This series of actions/sounds, despite its complexity, is usually parsed by our ear/mind as a single simple idea--for example, "play an A-flat staccato." "play a Bb, crescendo from ppp to ff "
To translate this idea of a score into the computer domain, is to posit the score as a kind of high-level-language which must be compiled into complex sequences of commands in a lower-level language.
Hence, I created "virtual instrument" programs (in the computer-language LISP) that take care of this. These programs in turn compile to programs read by the CMIX[2] package; that package in turn is written in C, which is eventually translated to machine-readable assembly-code, which is what actually produces the sound. The following example illustrates the chain:
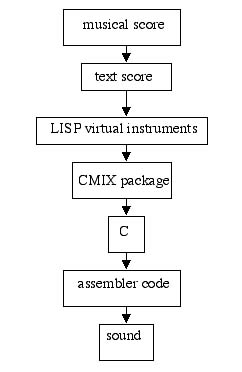
Here is part of a text-score that I might feed to the computer:
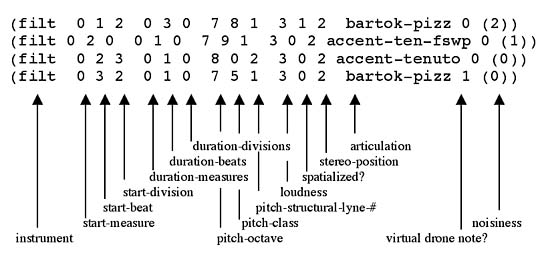
The score contains obvious data, such a note's start-time,[3] duration, and so forth; additionally there are more high-level command fields, most prominently articulation and, for the filter instrument in particular, noisiness.
The first note in this example has an attack-time of Measure 0, beat 1, division 2, and a duration of 3 beats. The pitch is in octave 7,[4] pitch-class 819, registral lyne 1[5]. Dynamics, (measured from 0 to 6) are next, followed by a flag indicating whether or not the note is spatialized (reverbed), and then stereo position, also from 0 to 5. This is followed by the articulation parameter, telling the interpreter how to make the note; a flag indicating whether or not the note is, structurally, a virtual drone note; and finally noisiness, an indication of the bandwidth of the filter (0 being thinnest, 5 being widest.)
When the LISP interpreter sees bartok-pizz, it’s being told to create the sound of the note in a certain way---one way amongst several possible filter articulations, such as tenuto-ellfilt, accent-tenuto, cresc, fp, etc. Each of these articulations may call for a different type of filter---for bartok-pizz, it’s a time-varying IIR filter, whose CMIX implementation is called FILTSWEEP, but for tenuto-ellfilt, for example, it calls the CMIX instrument ELL, which is an elliptical filter.
The various articulations differ procedurally as well. During the first few milliseconds of a bartok-pizz note, the center-frequency pitch of the filter varies wildly up and down, in a randomly determined way, eventually settling on the specified pitch of the sound. In terms of loudness, also, the sound is brought from an initial and very brief high level, to a final, quite low, level. It thus produces an illusion of a pluck or other percussive sound.[6] I should note that I call the articulation bartok-pizz mostly as a mnemonic signifier of inspiration, not to claim that the sound is a realistic duplication of an actual Bartok pizz.
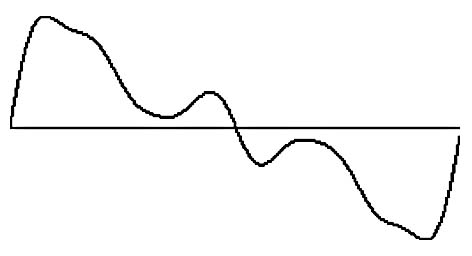
Another example, the articulation glissando, illustrates how determining the actions necessary to create a sound involves more complexity than one might think at first. Here we have a starting pitch, and an ending pitch, but it’s not just a matter of calculating a line between them, like so:

Instead, the curve itself, to sound most natural as a glissando, needs to look like this, perhaps:

In my particular instantiation I go further and "interrupt" this curve with wayward bends and changes of glissing speed, to make it more interesting, and finally, I have the gliss sit on the opening and final notes for a bit, so the ear can hear clearly the origination and destination of the glissando:

In acoustic instrumental music, whatever the articulation for a given note might be, that simple symbol is calling for a complex series of actions by the performer. At the computer, we need to emulate, if not the actions themselves and their sonic consequences, at least the complexity level thereof, as best we can, in order to obtain sounds that are as alive and life-like (even if also artificial and unfamiliar) as those of acoustic instruments.[7]
In summary, each of the virtual instruments used in this piece consists of a timbral source (for filter, this source simply consists of common filtered noise algorithms), and a set of articulations that manipulate and sculpt this source into notes that will form the music.
III.iii. Piano
The timbral sources for the piano and wwave instruments are less straightforward than for the filter instrument.
At its root, piano is simply a piano sampler or sample-player; that is, there are a number of pre-recorded samples which are transposed and/or looped appropriately to achieve the desired pitch and durations.
But there are some twists. First, all of the samples are taken from an "out-of-tune" piano I sampled several years ago. I only obtained 16 samples, of quite heterogeneous pitch registers, dynamics, and tone-colors. The pitches they represent are not evenly spread across the keyboard in any sense, as one would want them to be if creating a "professional" sampler. It is, in every way, a very uneven collection of sources.

Distribution of samples in a typical professional sampler.

Distribution of samples for Sand's piano instrument.
I worked with this weirdness. In a professional sampler, when an incoming MIDI signal (from a keyboard, for example) asks for a certain pitch, the computer looks for the nearest sample, so that the distortion of timbre produced by transposition would be at a minimum. But in the case of my home-brewed topsy-turvy sampler, the distance between the desired pitch and the pitch of the nearest sample used may end up being quite large (if the desired pitch is more than a major second away from the pitch of the sample used, the timbral distortion is audible), additionally, the desired loudness of a note may not match the performed loudness of the nearest sample; thus, I make no pretensions at timbral fidelity, and leave it possible that for any given desired pitch, any of the samples might be chosen to be transposed, adjusted to the appropriate amplitude, and looped to the desired duration. Thus if a pitch is articulated several times in a row, a new timbre is likely to be chosen for each repetition.
The second twist on the idea of a sampler is that, in order to achieve durations longer than the source sample, the source sample is not "looped". Instead, the sample is extended in a granular-synthesis[8] fashion: randomly chosen grains of the sample are overlapped for as long as the sound’s duration requires—thus the timbre of any given note is constantly changing in a satisfyingly random way.
This method allows us to develop interesting articulation realizations for tremolo and vibrato articulations. Instead of taking all the grains from the same initial sample, (as is done with the straightforward, ordinario articulation called accent-tenuto) each grain is taken (transposed appropriately of course) from a different sample. Vibrato is done the same way, with the transposition varying slightly for each grain.
Of course, each time a tremolo note is realized, the same basic procedures are used, but many parameters are varied slightly, randomly, during the note, and differently for each note--again, this is imperative in order to give the piece’s constituent sounds a sense of life and interest.
III.iv. Wwave
To create the wwave instrument, I dipped lower into the language-hierarchy: I wrote (or, rather, re-wrote) a CMIX instrument.
CMIX’s built-in WAVETABLE instrument produces time-un-varying harmonic timbres. One specifies the strengths of the sound's harmonics, and a wavetable is created. Each and every cycle of a given note are written with that wavetable, which can change only from note to note (and those changes require some programming effort). Hence if we ask for a sound with a fundamental of relative-amplitude 1.0, 2nd harmonic of relative amplitude .7, 3rd harmonic .5, 5th harmonic .2, 6th harmonic .06, and 7th harmonic .1, the resulting wavetable will look like:
This defines the timbre of the note, for the entirety of the note.
Real-world sounds don’t work this way: the relative strengths of the harmonics are constantly changing. Again, I wasn’t necessarily interested in imitating any particular real-world sound, but simply in injecting some of the "life-like-ness" of real-world sounds into the sounds in this piece.
Hence, in the new wwave instrument, the strengths of the harmonics change gradually, in relation to one another, over time, as the note sounds. The user can specify the average rate and amount of change. These can be specified as curves, so one can shape the inner-movement of the sound:
Within wwave's capabilities, I also included the idea of formants in an instrument. In a real-world instrument, the basic relative strengths of partials change as notes of different pitches are played, due to the resonances of the body and materials of the instrument filtering the sounds in various ways. An oboe, for example, emphasizes partials around 1400 and 2500 Hz. The ear detects these formant areas of lower or greater strength of partials, poking out of the sounds of many different pitches played on the instrument, and that is part of the way the ear identifies instrumental timbres. With wwave, one can specify a list of basic relative harmonic strengths and a list of formants when a note is played at a given pitch, the formants filter the harmonics appropriately.
With so many timbral possibilities, each wwave note requires a lot of data entry. Here is a typical CMIX specification of a wwave note in Sand:

Avoiding having to be directly responsible for this kind of low-level complexity is where the higher-level "score" language illustrated above comes in handy once again: The whole note listed above could be generated, via the LISP virtual instrument software, by this note in the text-score:[9]
(wwave 0 1
0 8 5 2 3 1 3 vibrato 0 ebclar)
III.v. Orchestration
As I wrote and realized the music, I learned to orchestrate for these instruments. Just to give a few examples of rules-of-thumb that I learned through trial-and-error: accent-tenuto (which is the most ordinario articulation for any of the instruments) wwave notes are best deployed in very short durations (i.e. staccato), being especially effective in rapid, registrally-far-flung sequences. (Section 52, near the "climax" of the piece, provides a good example--although all of the instruments are more or less doubling on the same line at this point, wwave's notes dominate the timbre.) As longer durations, they threaten to sound dull and lifeless. On the other hand, wwave’s more bizarre articulations, like vibrato and nasty-am-tremolo, as they contain more activity and change of parameters per unit-time, can be deployed as longer durations. The instrument piano tends to be softer than the other instruments, and its dynamics and pitches are less accurate (being based on extremely varied samples that are themselves often made up of dissonantly beating tones, so that assigning them an exact "pitch" is quite difficult). Thus, when I want a very clear, well-tuned instantiation of a harmony, I won't use piano. Filter’s articulation accent-ten-fswp (standing for "accent-tenuto using the FILTSWEEP CMIX instrument") works very well for notes of almost any duration or dynamic. On the other hand, tenuto-ellfilt articulations are appropriate for longer durations where a touch of misterioso is required.
III.vi. Musique Concrete Gesture Engine
So far we've been discussing what I call the "intentional pitch" instruments in the piece. With these instruments, I ask for certain pitches, the instruments produce them (usually), and thus, I can work with pitch structures such as the serial ones described in part II of this Essay.
Another layer of this piece involves musique concrete sounds, sounds of a percussive, usually non-pitch intent (though pitch is always present in some way, of course). In order to arrange an effective coupling of the intentional pitch and musique concrete instruments, I built a "gesture engine" that would allow me to specify abstract musical shapes, gestures and event sequences, leaving the engine to find various appropriate sounds to fill in the gesture. The engine can also find sounds containing prominent partials at desired pitches, so that they can be "matched" with current events in the pitch-structure.
To understand this idea fully, I will recount my experiences composing gestures in the realm of computer music, especially in the realm of musique concrete.
When I first started to realize music with the computer, the following would often occur: I would think and hear a gesture in my head, "oomph," and attempts to realize that gesture, through mixing of samples, synthesis, processing, programming, and so forth, would result in "aaamph" (so to speak)--not quite (or sometimes quite distant from) what I originally wanted. This is a problem that is much less likely to occur with acoustic instruments, because, first of all, I know what acoustic instruments can and can't do, what different sequences of events played on a given instruments will sound like, and so on; second of all, there is a whole set of received wisdom about idiomatic gestures for different instruments that constantly, (whether I like it or not) informs and affects the way I write for those instruments.[10] With computer music, this is not the case: it's much more of a clean slate, and though I make [what I hope are] reasonably well-educated guesses, when I deploy sonic materials in a certain way, I am nevertheless likely to get something completely unexpected.
To deal with this problem, I take less of an "I've got to get this gestural effect" kind of approach, and more of a "Let us experiment with what this machine does; generate some musical material, consisting of gestures whose characters and affects we can't quite predict; then we will see how we can modify the musical contexts in which we place those gestures, so that the gestures 'work' (musically and dramatically speaking)."
The experimental process of the "generation of some musical material" I mention above is partially an intentional one, partially an arbitrary one: I might begin by trying to get a certain gesture out of the machine; what comes out is something different from what I had in mind originally. I may then try to modify the gesture to get it closer to what I wanted originally, changing the parameters I gave the machine to create it in the first place; but eventually, I change paradigmatic gears entirely, and I begin to think, instead of how to achieve gesture X to fit context A, how to shape context A to accept or fit gesture X. In other words, creating the context that will make things seem as if the accidentally-created gesture was not accidental, but created for the context.
This is often part of my composing process in works for acoustic instruments as well, but it has a special relevance for computer music, since the relationship between what I tell the computer to do and the resulting sound is far less well understood than the relationship between what I tell an acoustic instrumentalist to do, notationally, and what sound comes out. The plethora of unexpected material coming out of the machine demands this approach.
Of course, as one continues with this looser, more experimental approach to sound and sound-gesture creation, something that starts to resemble a "tradition" is built up, amazingly fast. One learns the kinds of effects that most often result from certain methods of sound synthesis, or certain kinds of combinations of samples, on the computer. Frequency modulation, amplitude and ring modulation, physical models of instruments, different types of sound processing, and so on, all have their characteristic tone colors or families of tone colors; and, extrapolating from there, typical resultant gestures or families of gestures, with corresponding emotive associations, arise from the use of a given computer-music tool.
Computer-music history itself, is, in a large part, the story of a series of discoveries of new sound generation techniques, each followed by a flurry of excitement and new pieces using the technique; often the excitement over the technique for its own sake dies off fairly quickly, and the technique is then absorbed into the community as simply another tool for making sound.
This lesson of history I have taken to heart and hence I try to focus my compositional energies not (entirely) on the method of synthesis of a particular gesture, but on its harmonic, rhythmic, and timbral content/context. I deliberately do not seek out "new sounds," but rather, I try to use old ones, to combine and re-combine them in a rapid kaleidoscopic fashion to produce event-complexes in which the interaction of different sound components, though they may each be individually familiar, yields a combined event-complex that is something new in a subtle, yet striking way.
Thus, in my first mature computer-music work, Ow, My Head, I decided from the start not to utilize any kind of synthesis or processing at all, but to deploy only raw, unprocessed, recorded musique concrete sounds from the environment in the musical fabric. In all of my pieces using this type of material, the sounds are usually recorded in one place (in the case of this piece, the house where I grew up in the suburbs of Philadelphia); though this certainly does not provide any source of immediate sonic or musical "unity," it does provide for me, psychologically, a desired spiritual unity--a unity of spiritual source, so to speak. (Sand's samples were recorded in Westport, Massachusetts.)
I'll say a word about why I chose to use concrete sounds in particular (out of all the choices of material one has with computer-music composition). Emotionally, it is the effect of displacement of a sound, a sound with very clear origin, from that origin, that I find fascinating about the use of "found sounds." Each sound brings with it an illusion of its original space or place, be it a kitchen, a washroom, a subway train, or whatever. Yet the sounds are brought together in a "musical" space. The interaction between these spaces in the mind of the listener I find to have a powerful emotional effect. It is similar to the effect one experiences watching a movie with bright, sunny, images: sometimes the mind loses itself in the illusion of the sunniness, then it realizes that all of this is taking place in the darkness of a movie theatre, possibly in the dead of winter around midnight. I like the almost frightening, spooky aspect of this paradox; it is the emotional basis of my attachment to concrete sounds.
On a more technical level, musique concrete is (still) a wide open field of discovery, in terms of the idea, mentioned above, of combining sounds together rhythmically, harmonically, and timbrally to produce new event-complexes or meta-timbres. I am asked, about Ow, My Head, how I processed (filtered, reverbed, delayed, etc.) or synthesized certain sounds; but, in fact, there was no processing, no synthesis; instead, the particular combinations of raw sounds in the piece, achieved only through relative rhythmic and amplitude adjustment, produced the "new" metatimbres.
The piece was composed in small blocks, each consisting of a sequence of only a few gestures (something analogous to a phrase). Later, the blocks would be joined to form sentences and, eventually, a complete form for the work.
The process of composing a gesture, or a small sequence thereof, went, in general, something like this: "spray" a random set of sounds (a subset of the complete set of about 200 sounds, varying in duration from 0.2" to 5" or so) into a mix.
The tricky part about these mixing images is that pitch-content is not displayed in any way. (The display is solely of amplitude/time.) With found sounds, pitch-content is often complex, so that a simple "score" representation (i.e.--each sound having a single fundamental "pitch") would be problematic. In the case of this piece, I relied mostly on my ear and aural memory to keep track of what sounds were associated with what pitches, and thus to construct contours and harmonic combinations of the pitch-contents of different sounds.
The next step was to hone the "sprayed" mix that appeared. There are a few common methodologies I used to hone the randomly-generated sound-sequences:
1) Line up the attack-points (or points of high amplitude) between selected sound objects, like so:
Since the ear will often hear multiple sounds with the same attack-time as one single, new, combined sound or timbre, these kinds of events probably account for people's questions as to what processing and/or synthesis techniques I used: the new events seem familiar, yet skewed in some way.
2) Frequently, I will use these simultaneous-attacks as goals of, or origins of, rhythmic activity, for preceding or proceeding sound complexes. Then I will use increasing or decreasing density of sounds (i.e. accelerando or decelerando), as rhythmic patterns of approach to, or departure from, these goals.
Hence, the music, (especially in this piece) often becomes a series of waves. I like to think of my use of waves as being analogous Elliott Carter's wave-forms in his large ensemble pieces (Concerto for Orchestra, Double Concerto, etc.). As in Carter’s works, some of the waves in Ow, My Head are composed of simultaneous overlapping tempi.
3) Depending on the particular sounds used in a particular context (phrase), I use timbral/harmonic characteristics of the sounds themselves to guide their placement in relation to one another. Often this amounts to something similar to common-tone-modulation in tonal music; we might call it "common partial" modulation. Thus, two successive sounds may be very different, in terms of features such as attack hardness, fundamental pitch, presence or absence of internal repetition or agitation, etc.; but the ear will still hear these timbral/harmonic connections between them. Or, a certain sound might "fade in" from another's timbre, entering in a smooth blend (having several common partials) with the first, thus forming a line begun by the first sound. A chain of such relationships can create a continuous line of timbral change. Noisier sounds, with no strong individual partials, can be thought of as frequency bands of noise in a given register. Thus they can lead smoothly to other, acoustically and spectrally similar sounds.
In either case, the continuity of certain partials allows the ear to hear the sequence as developmental, and is thus an important way of achieving the coherence of a gesture or phrase.
Another kind of progression illustrates the exploitation of a psychological-analogy relationship: in Ow, My Head (at 4:07) the sound of a toilet flushing, acoustically basically a band of noise, and the sounds of vocal weeping (vocal tones with downward glissando) are heard in counterpoint. To my ear, this meshing works particularly well, and the reason is not an acoustic one, but rather, that both sounds communicate a sense of down: toilets flush downwards, and weeping involves downward motion (of musical pitch, spirits, tears, and so forth.)
One of the main ideas for my next computer-music work, Duude, came from my desire to achieve maximum rhythmic density via this "spraying and neatening-up" procedure. In Ow My Head, I had been more concerned with the idea of individuated, clear musical gestures, or small sequences of gestures. In Duude, for certain sections of the piece, I wanted to achieve a massive gestural density---one where the individual sounds could still be more or less clearly made out, but where their toppling over one another would create a continuous frenetic web of sounds.
As in Ow, My Head, I had a collection of found sounds, about 300 of them, the basic material for the work. Most were very short, objects (bottles, plates, silverware, etc.) being scratched, hit, rubbed, etc. I decided that these high-density "wads" of concrete counterpoint would be, at most, a minute long each, a minute into which I'd pack all 300 of my basic sounds. The procedure for making these “wads” thus became one of randomly spraying the 300 sounds into the first minute of the mix; then, as in Ow, My Head, adjusting the timing of the sounds in the "wad" so that each sound would flow, lead, or leap into the next one(s).
After Duude, while composing works for acoustic instruments, I continued to think on some of the questions raised by my computer-music endeavours, especially by the more musique-concrete-based Duude and Ow. I wanted to get back to "achieving gesture X to fit context A," rather than making gesture X from randomly selected materials and then "shaping context A to fit gesture X." I wanted to accomplish this with collections of raw, unprocessed found sounds.
Much of the computer-music world is concerned with processing a sound until it becomes un-recognizable. Recognizability and association may result in an affect that is too sentimental or "cheesy." This happens when the most relevant thing (or even the only thing) that the listener hears in the individual sounds in a mix are their associations. In other words, the listener thinks only "Huh. . .these are pots from Christopher Bailey's kitchen. . ." This is a worst-case scenario, and because of even the shadow of this possibility, many computer-music composers are driven to "hide" their sounds behind a wall of processing and transformation. This "safety procedure" does not interest me: I do not want to rid the sounds of all recognizability and therefore all associations; instead, my goal is to produce music where overall gestural shapes and phrases take precedence over the autonomy of the individual sounds, where their individuality is sacrificed to these greater musical wholes; and yet, those individual associations and references are still there. This leads to a multi-level musical experience---structural, musical listening, in terms of how a phrase or sentence works, and associational listening---"this finely-crafted phrase. . . just so happens to be made of pots from Christopher Bailey's kitchen. . ."
The desire for some regularity in producing "finely crafted phrases" out of found sounds led to the creation of the musique concrete database engine.
We first describe a phrase as a sequence of events, each of whose parameters can be specified exactly. We store information about all the sounds in our source collection in a database. We can then ask for the computer to search the database, matching the specified parameters of an event against the parameters of sounds in the database, thereby ultimately retrieving an appropriate sound for each particular event.
What would such a database look like?
Here is Sand's.
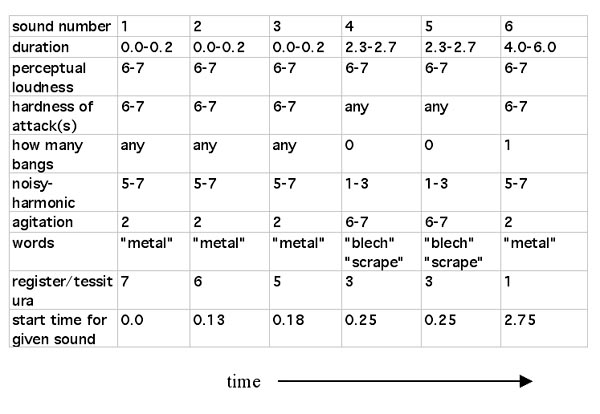
Each sound is described in terms of 11 parameters.
The first, filename, is simply information about where the sound-file lies on the computer disk. Duration, measured in seconds, is self-explanatory. Pitch indicates one or more strong pitches or partials in the sound---most often, the fundamental or first harmonic. (It is indicated here as 19tet pitch-class number) Of course, some sounds have no clear pitch, and therefore this parameter is left empty. Loudness is not about sheer amplitude or volume, but rather perceptual loudness---a light whisper is a qualitatively soft sound even when highly amplified. This parameter is measured from 1-7, as is attack-hardness, describing the "violence" of the beginning of the sound---whether it fades in, enters with a bang, or something in between. The 1-7 range applies to many of the parameters.
The reader might recall, from the discussion of Ow, My Head, the idea of "lining up attack-points between different sound objects." (See example 3). The bangs-list is a list of those attack-points. Later, we can use this information to have the machine line up those points automatically.
Noisiness/harmonic is also more or less self-explanatory: a voice or a bell would be a harmonic sound (value of 1), crumpling paper would be noisy (value of 7). Rubbing a washboard, producing both a pitch and a fair amount of noise, would be somewhere in between. Color describes whether the sound tends toward being "dark" (value of 1) or "bright" (value of 7). Agitation describes the internal state of the sound during it's duration: is there much movement and change (for example, vigorous rubbing or scraping) (value of 7), or is there simply a decay (a bell rings) (value of 1 or 2), or something in between? Tessitura/register describes the general pitch register of the sound (even if it is too noisy to have an exact pitch), from low (1) to hi (7).
Finally, material/category remains as a sort of catch-all "semiotic" parameter, describing associations, concepts or words that the sound brings to mind. Thus, often it is simply a matter of material (e.g.---"metal", "glass”) and/or action ("creak", "scrape"); sometimes it describes some important musical characteristic of the sound (e.g. "rhythm" if the sound is "rhythmic").
Measuring some of these parameters from 1-7 might seem very crude, but the crudeness is appropriately matched to the extreme heterogeneity of the materials. For example, what would be softer, a whisper or a recording of soft, distant ocean sounds? We'd all agree that they are both soft sounds. To get more specific than that would tend towards the highly arbitrary. Thus 1-7 seemed like a reasonable compromise.
You might imagine how this database would be used.
There are two implementations of the engine: the first one I made for purely time-fixed concrete works, the second implementation of the engine was specifically for use with the piece Sand. I'll describe the former, and then the ways in which the latter is different.
We can essentially think of a musical gesture as a sequence of events, each event being described in terms of one or more of those 11 parameters. Thus a simple gesture might be: 3 short, high sounds, with hard attacks, descending in register, made of glass or metal; a couple of simultaneous, longish (2" or 3") highly agitated mid-register sounds; slamming down into a low metallic sound, with a hard attack, not agitated but with a very long decay.
Here is a quasi-pictogram of the gesture:

To the computer, we feed a "spreadsheet" of the same gesture:
The computer, when fed the "spreadsheet," looks at each column, figures out what parameters a sound would need to have to satisfy the criteria of that column, and grabs a random sound from the collection that satisfies those criteria. It then places the sound in a mix, where the composer may modify the order of the sounds, delete sounds, or whatever. Furthermore, it is easy to generate 10 or 20 versions of a given gesture, each a different attempt by the computer to realize the specified gesture with a different combination of sounds; hopefully one of those combinations will be the desired gesture. (Of course, another possibility is that the computer will come up with something pleasantly unexpected.)
Finally, it is also possible to specify what I call a bang-tree. This is a special rhythmic specification that arises from the bang-list parameter mentioned earlier.
Let us begin with the following pictogram:
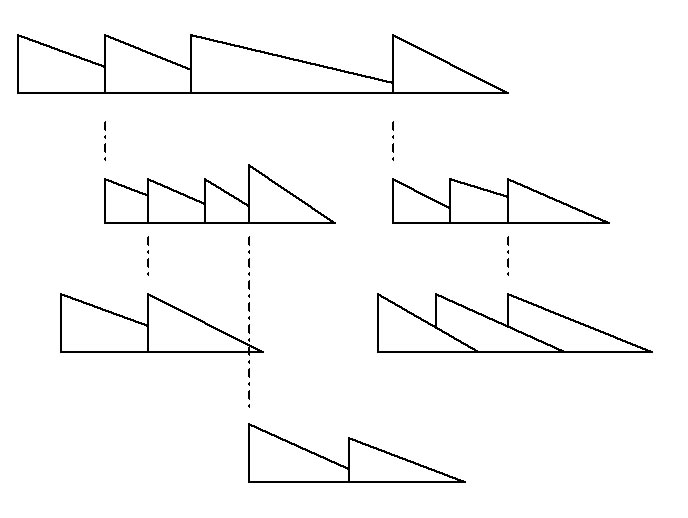
You can see that the idea is one of a gesture whose sounds relate rhythmically through their common peaks or attack-points---as discussed in Ow, My Head.
We can then feed, to the computer, a list of the qualities of these sounds (as in the example above) and a bang-tree: a list of how the bangs in the sounds relate in time. A bang-tree takes the following form:
(mother-sound (child-sound mother-bang child-bang)
(child-sound mother-bang child-bang))
(mother-sound (child-sound mother-bang child-bang)
(child-sound mother-bang child-bang)). . . . . . etc.
Thus, in the example, sound 0 is the "mother" of sounds 1 and 2. Then, in turn, sound 2 is the mother of 4 and 5, and so on. 1, a "child" of 0, attaches its bang #0 to sound 0's bang #3. Sound 3 attaches its bang #2 to 1's bang #2, and so on. Thus we get, as the whole tree:
(0 (1 3 0) (2 1 0))
(1 (3 2 2))
(2 (4 1 1) (5 3 0))
The computer's task is to finds sounds with the appropriate number of bangs, (as well as any other qualities we care to specify), and mix them as we request, placing them in time so that the appropriate bangs line up.
In Sand, because of the possibility, using the interface, for the listener to change the tempo at will, the bang-tree idea could not be implemented.[11] Instead, each sound in the concrete layer of Sand is entered as a note, using a special html/php entry sheet.
Note that we can vary the amplitude of the sounds; we can slap amplitude envelopes on them; we can ask that a sound "cut in" right at one of its bangs (very helpful in tight rhythmic passages).
Some examples of the features of this system in action in Sand:
1) Because the "intentional pitch" instruments (wwave, piano, filt) include articulations that are very noisy in character, we can get a continuum between harmonic and noisy sounds, in both the concrete and intentional-pitch layers. Thus we can have passages like the latter half of Section 3 of the piece, where noise and pitch seem to fade in and out of one another.
2) One possibility, that I found myself taking advantage of quite often, is asking for streams of many short, cut, hard-attacked sounds of various dynamics, for a kind of constantly renewing "drum-machine" effect. We can hear this in Sections 9-10.
3) In Sections 11-12, the pitches of "pot fanfares" work in conjunction with pot-fanfare imitations in the piano instrument.
4) Sometimes one or one type of concrete sound guides what's happening in the pitch instruments. In Section 33 a conflagration of voice sounds dominates the concrete texture. The pitches and rhythms articulated by the "intentional-pitch" instruments attempt to "line-up" with the pitch-classes in the voices. A clearer example of this, with just one voice sound, can be heard in Section 57. Similarly, in Section 36, a long, descending door-creak leads a number of intentional-pitch gliss articulations in the wwave and filter instruments down into the basement.
5) Sometimes specific concrete sounds are so very "pitched" that I use them, harmonically, to help parse the pitch structure. At the opening of Section 13, "bell" sounds ring out in beautiful diatonic sonorities. The pitch-arrays in this section warp themselves to fit around them.